Hola, existen diferentes tipos de Números. Aqui, vamos a comenzar.
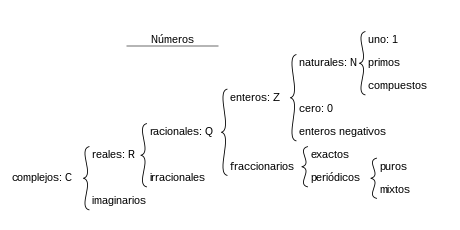 |
| Así es como esta Representada y/o formada la Clasificación de los Números |
Números Naturales!
Los Números Naturales sirven para contar elementos de un conjunto, y están designados por N, Aquellos números naturales son:
- Mayores que 0
- No tienen decimal ni nada. Son exactos.
- Los números nunca acaban.
N = {1,2,3,4,5,.....∞)
Sirven para contar.
Acerca del Cero, con los Números Naturales.
NOTA: El Número Cero no es Número Natural, porque es el Elemento Neutro de la Suma y Resta. y en este Caso, no es Positivo ni Negativo, Es Neutro!
Aunque el Cero se puede considerarse el Número que corresponde a la ausencia de los mismos. Dependiendo del área de la ciencia.
El Número Uno(1)
El Número Uno(1) es el Primer Número Natural que es Sucesor de 0, y antecesor de 2
Al Sumar 1, Sale su Número consecutivo. (El Que sigue)
Características del Número Uno(1)
- El Número 1 es el Elemento Neutro en Multiplicación y División, osea, que si multiplicas o divides 1, te vuelve a dar lo mismo.
- El Número Inverso del ''1'' es el Mismo, porque ''1 / x'' con ''x = 1'' Vuelve a dar ''1''
- El Único divisor del 1 es el Si mismo
- Todos los Múltiplos del 1, son todos los Números Naturales.
- El 1 es divisor de todos los Números
Ejemplos:
27 * 1 = 27
52 / 1 = 52
Los Números Primos
Un Número primo es un número natural mayor que 1, lo cuales que tienen solamente dos Divisores y esos dos Divisores vienen siendo el 1 y el si Mismo. Esos números se contraponen con los Números Compuestos son como elementos Complementarios. (Osea cuando uno si ocurre y el Otro no)
Aqui esta una lista de los Números Primos del 2 al 1000
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 ,83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
Como ven, esos son todos los Números Primos menores que 1,000 y en este caso 168 Números son Primos
El Número 0 y 1 no se consideran primos ni compuestos, porque el ''0'' como es el Elemento Nulo, no tiene ningún divisor y el ''1'' No mas tiene un Divisor, lo cual ese Divisor seria ''1''.
- Todos los Números Primos son impares excepto el 2 (que es par).
- Siempre un Número Primo tiene 2 Divisores
- Los Números Primos no aparecen en múltiplos de un Número Compuesto.
Ejemplos:
Los divisores del 457: son el 1 y 457(si mismo)
Los divisores del 761: son el 1 y 761(si mismo)
Los Números Compuestos
Un Número Compuesto: Es un numero Natural diferente a 1 que no es primo. Y tiene por al menos 3 Divisores..
Los Números Compuestos son lo contrario de los Primos.
Los Números Compuestos del 4 al 100 son:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100
Si te das cuentas Allí no hay números primos..
Aquellos Números que tengan 3 o 4 Divisores se les llaman Semiprimos, lo cual los Semiprimos son obtenidos al Multiplicar dos Números Primos cualesquiera y tienen 3 o 4 Divisores.
Ejemplo: 17 y 31 son Primos
17 * 31 = 527
En este caso, 527 es un Número Semiprimo!
Los que tienen mas de 4 Divisores, ya no se consideran Semiprimos!
¿Has visto que muchos de los Compuestos tienen al menos 4 Divisores?, Aquí hay Números Compuestos con 3 Divisores!
Esos números que tienen 3 Divisores son aquellos que se obtienen al elevar un Número Primo al Cuadrado.
NOTA: También los Cuadrados de los Primos, también son Semiprimos!
Ejemplo: 11*11 = 11² = 121.
Los Divisores del 121 son 1, 11, 121
En este caso.
1 es el Divisor Predeterminado para cualquier Número.
11 es el Número Primo.
121 es el Cuadrado del Primo
Números Enteros.
Los Números Enteros (designados por Z) son los que incluye a los Números Naturales y a los Menores que Cero(0), incluyendo al Número Cero(0) no tienen parte decimal y respecto a los Números Naturales.. Los Números Enteros pueden ser Negativos y Positivos
Asi va la Sucesión de los Números Enteros
Z = {-∞,.....,-5,-4,-3,-2,-1,0,1,2,3,4,5,.....,∞}
Ejemplo: -127 es un Número Negativo y Entero pero NO es Natural. porque los Números Naturales sirven para contar y cuando el Número es Negativo ya NO es natural, También los Enteros son Positivos, Todo número natural es Entero :)
Los Números enteros también se pueden expresar como Temperatura o Altura, y para muchas cosas, Los números negativos pueden ser de útil.
Valor Absoluto
Cuando el Valor es Absoluto, se le quita el Signo y siempre es Positivo, si no tiene parte decimal.
Ejemplo: |-10| = 10
En este caso el Valor Absoluto de un Número Negativo es Positivo
|±x| = x
|±5| = 5
|15| = 15
|-32| = 32
|±17| = 17
|21| = 21
|-22| = 22
y = |x|
x = {-5,-4,-3,-2,-1,0,1,2,3,4,5}
y = {5,4,3,2,1,0,1,2,3,4,5}
y = |x|
x = {-5,-4,-3,-2,-1,0,1,2,3,4,5}
y = {5,4,3,2,1,0,1,2,3,4,5}
También se puede crear una Formula donde solo Permita números negativos con la Función del Número Absoluto. seria asi: -|x|
-|±x| = -x
-|±9| = -9
-|23| = -23
-|-31| = -31
y = -|x|
x = {-5,-4,-3,-2,-1,0,1,2,3,4,5}
y = {-5,-4,-3,-2,-1,0,-1,-2,-3,-4,-5}
-|±x| = -x
-|±9| = -9
-|23| = -23
-|-31| = -31
y = -|x|
x = {-5,-4,-3,-2,-1,0,1,2,3,4,5}
y = {-5,-4,-3,-2,-1,0,-1,-2,-3,-4,-5}
Números Racionales
Un Número racional (Designado por Q) es un número que se puede representar como el cociente de dos números enteros al hacer una División Entera y que salga un Resto es decir, una fracción común a/b con numerador a y denominador b distinto de cero. a aquellos tipos se les pueden expresar como Fracción lo cual vendrian siendo números Fraccionarios.
Ejemplo: 15/4 es Racional porque 15 entre 4 da 3.75 (Cociente: 3, Resto: 3) en este caso también terminaría siendo una División Entera (las que terminan teniendo un resto) en este caso se expresa como ''15/4'' es irreducible; porque el Máximo común divisor de 15 y 4 es ''1''
También un Número Racional puede tener una Parte Decimal, puede ser Exacta o Periódica Este conjunto de números incluye a los números enteros (Z), y es un subconjunto de los números reales (R). En este caso se puede expresar como Decimal. Ej: 2.56, 1.67, 6.4, 2.44444..
Ejemplo: 15/4 es Racional porque 15 entre 4 da 3.75 (Cociente: 3, Resto: 3) en este caso también terminaría siendo una División Entera (las que terminan teniendo un resto) en este caso se expresa como ''15/4'' es irreducible; porque el Máximo común divisor de 15 y 4 es ''1''
También un Número Racional puede tener una Parte Decimal, puede ser Exacta o Periódica Este conjunto de números incluye a los números enteros (Z), y es un subconjunto de los números reales (R). En este caso se puede expresar como Decimal. Ej: 2.56, 1.67, 6.4, 2.44444..
Aritmética de los números racionales
Operaciones con Números Racionales (Fracciones)
Se define la Suma como: a/b + c/d = ''ad + bc'' / ''bd'',
y recuerda que si el MCD de ''ad+bc'' y ''bd'' es mayor que 1. Allí si se puede reducir la Fracción y seria una Fracción Reducible.
Se define el Producto como: (a/b) * (c/d) = ac / bd
Los Numeradores y Denominadores se multiplican entre si y dan a conocer ese Resultado.
Se define la Resta como: a/b - c/d = ''ad - bc'' / ''bd''
Es lo mismo que la suma solo que es la Operación inversa de la Suma. y aquí las cosas cambian en la Resta. respecto a la Suma
Se define el Cociente como: a/b ÷ c/d = ''ad'' / ''bc''
Se saca el Producto de los Números cruzados. y así queda. osea que se cruzan.
Números Fraccionarios
Ya hemos hablado de los números Fraccionarios recientemente, los que estan formados en Fracción
Clasificación de Fracciones
Fracción mixta: Suma que se abrevia con un Entero y una Fracción Propia:
a + b/c = >1(Mayor que 1)
Fracción Propia: Fracción donde el Denominador es mayor que el Numerador, también vendría siendo un Número Racional entre el 0 y 1, Ejemplo: 5/6, 3/7, 4/5, 6/11
a/b, donde a < b (''a'' menor que ''b'')
Fracción impropia: Fracción donde el Numerador es mayor que el Denominador, también vendría siendo un Número Racional mayor que 1. Ejemplo: 13/6, 17/7, 10/9, 15/8
a/b, donde a > b (''a'' mayor que ''b'')
Fracción reducible: Fracción donde el numerador y denominador no son primos entre si, y cuyo Maximo Comun Divisor es mayor que 1, y se puede reducir y simplificar, Ejemplo: 4/8, 9/12, 21/56
a/b, donde MCD(a,b) = <1 (Maximo común divisor mayor que 1)
Fracción irreducible: Fracción donde es lo opuesto a lo Reducible. Allí es cuando el numerador y denominador son primos entre si, y ya no se puede simplificar mas. y cuyo MCD es 1, Ejemplo: 6/11, 9/16, 11/18
a/b, donde MCD(a,b) = 1 (Maximo común divisor igual a 1)
Fracción inversa: Fracción obtenida donde se le obtiene su Inverso, en este caso se Intercambian los valores del Numerador y Denominador se le saca su Inverso o Reciproco, Ejemplo: 7/6 y 6/7; 1/5 y 5
''a/b'' y ''b/a'' son inversos. donde el Inverso de ''a'' es ''1/a''
Fracción aparente o entera: Fracción cuando intentas dividir el denominador entre el numerador te sale un Número entero. es decir no tiene parte decimal y Terminaria siendo un Número entero. Ejemplo: 14/7 = 2; 18/6 = 3; 8/2 = 4
a/b, ''b'' sería múltiplo de ''a'' y ''a'' sería divisor de ''b''
Fracción equivalente: Fracciones que tienen el Mismo Valor, Ejemplo: 3/7 = 6/14 = 9/21 = 12/28 = 18/42 = 24/56
Fracción homogénea: Fracciones donde tienen el Mismo Denominador, Ejemplo: 2/7 y 4/7; 6/19 y 13/19
''a/c'' y ''b/c'' son Fracciones Homogéneas
Fracción decimal: Fracción donde el Denominador es una Potencia de 10, Por ejemplo: 3/10, 47/100, 357/1000,
En este caso sería asi: ''a / 10ⁿ'' donde ''a'' es un Entero y ''n'' un Numero Natural.
Números Decimales
Los Números decimales son los que se expresan asi: 3.4, 6.14, 9.578
 |
| Clasificación de los Números Decimales. También pertenecen a un Subconjunto de los Números Racionales. excepto el de ''no periódico'' que pertenece a los Números irracionales. |
Los Decimales Exactos
Los Decimales Exactos son aquellos que en su Parte decimal tienen un número finito de cifras se les denominan ''números decimales exactos.''
Ejemplos:
- 247/80 = 3.0875
- 5243/1250 = 4.1944
NOTA: El Número del Denominador se puede obtener usando Potencias de 2 y 5 por ejemplo: 2000 = 2⁴ ∙ 5³
Los Decimales Periódicos Puros
Los decimales Periódicos Puros son aquellos que en la Parte decimal tiene un Número Infinito. se repiten inmediatamente después del separador decimal, por ejemplo:
En este caso la Fracción 1/3 se representa 0.
En este caso la Fracción 1/3 se representa 0.
5.7 = 5.77777777 = 52/9
3.34 = 3.34343434 = 331/99
0.8 = 0.88888888 = 8/9
1.63 = 1.63636363 = 162/99 = 18/11
NOTA: El Periódico esta en Negrita
Los Decimales Periódicos Mixtos
Los decimales Periódicos Mixtos son aquellos que en la Parte decimal tienen una parte no periódica, denominada antiperiodo y otra periódica
Ejemplos:
0.83 = 0.83333333 = 75/90 = 5/6
0.51 = 0.51111111 = 46/90 = 23/45
0.632 = 0.632222222 = 569/900
0.287 = 0.287878787 = 285/990 = 95/330
0.394 = 0.394949494 = 391/990
0.632 = 0.632222222 = 569/900
0.287 = 0.287878787 = 285/990 = 95/330
0.394 = 0.394949494 = 391/990
NOTA: Lo negrito quiere decir la Parte Periódica y lo Subrayado la Parte Antiperiodica. Ten cuidado de no confundirte.
Números Irracionales
Un Número Irracional, es aquel que no se puede representar como una Fracción m/n, Donde ''m'' y ''n'' son Números Enteros pero ''n'' es diferente a cero(0), Es cualquier número Real que no es Racional :)
No se pueden expresar en Notación Científica.
En este caso al Sacarle la Raíz Cuadrada a un Número por ejemplo.. la Raíz Cuadrada de 2 (√2) es un Número Irracional.. Porque no se encuentra el Limite de los Dígitos Decimales
√2 = 1.414213562373095
Si la Raíz Cuadrada de 2, se multiplica por si mismo, va a dar 2.
Tambien al sacar el Logaritmo de un Número puede resultar Irracional.. Casi siempre
La Raíz Cuadrada de 4, no es Irracional, si no Natural. Porque 2² = 4 y al sacarle la Raíz Cuadrada de 4, el Número es 2: porque 2 * 2 = 2² = 4
√4 = 2
Números Trascendente
Un número trascendente(también conocido como número trascendental) es un tipo de número irracional que no es raíz de ninguna ecuación algebraica con coeficientes enteros no todos nulos. Es decir la Solución de una Ecuación de Segundo Grado o mas.. No llega a ser Transcendente..
Lista de Números Trascendentes
- Número π = 3.141592653589793
- Número e: 2.718281828459045
- In(2) = 0.693147180559945 (Logaritmo Natural de 2)
Números Algebraicos
Un Número Algebraico es cualquier número real o completo que es solución de una Ecuación algebraica que cuyo grado del Polinomio es igual o mayor que 2 (x ≥ 2)
En este caso, Siendo de segundo, tercer o cuarto grado, etc.. Un número algebraico viene siendo la Solución de las Ecuaciones de un Grado igual o mayor que 2.
Ejemplos:
- Todos los números racionales son algebraicos porque toda la fracción de la forma a/b. es la solución de bx - a = 0, donde, ''a'' y ''b'' son enteros.
- Algunos números irracionales tambien son algebraicos. Por ejemplo en la Operación: x² - 5 = 0, La Respuesta viene siendo: √5 (Raíz Cuadrada de 5), Lo cual las Raices pueden ser Números Algebraicos.
- El Número imaginario (i) también es Algebraico porque viene siendo la Solución de la Ecuación de: x² + 1 = 0
Números Reales
Los Números Reales, vienen siendo los números que si existen y tienen un Valor. En este caso incluyendo a los Números Naturales, Enteros, Racionales e Irracionales.
 |
| La Recta Real de los Números Reales. |
Números Complejos
Los Números Complejos son una extensión de los números reales. Aquellos Números pueden ser la Solución de Ecuaciones Cuadraticas o mas alla. en este caso, Las Ecuaciones Cuadraticas tienen un Discriminante que es: b² - 4ac, donde ax² + bx + c = 0, En este caso cuando la Discriminante es Menor que 0 (<0), La Ecuación Cuadrática, no tendra ninguna Solución real, si no dos Soluciones Complejas, donde no son reales los Números
Mas informacion acerca de una Ecuación Cuadratica.. Clickeame :)
Los Números Complejos no tienen un Valor Real. y no se puede saber cuanto valen.
Número Imaginario
Un Número imaginario, es aquel que es un Número Complejo y no real.. En este Caso el Número Imaginario equivale a: √-1 (Raiz Cuadrada de -1)
i = √-1
En este caso resulta ser al hacer Ecuaciones no lineales.
Por ejemplo: x² + 5 = 0
1) x² + 5 = 0
2) x² = -5
3) x = √-5 (Raiz Cuadrada de -5)
4) x = i√5
En este caso la Raiz Cuadrada de 5. Mas se expresa como: i√5
i = √-1
En este caso que es lo mismo que √-5 porque: (√-1)(√5) = √-5
Pero no siempre al hacer Operaciones con el Número Imaginario te sale un Número Complejo, puede llegar a ser Real:
Por ejemplo al Multiplicar ese Número por si mismo: (i)(i) = i² = -1
El Número Imaginario al Cuadrado da -1, Porque el Número Imaginario equivale a la Raiz Cuadrada de -1
2i = √-4
3i = √-9
4i = √-16
5i = √-25
(2i)² = -4
(3i)² = -9
(4i)² = -16
(5i)² = -25
(2i)³ = -8i
(3i)³ = -27i
(4i)³ = -64i
(5i)³ = -125i
(2i)⁴ = 16
(3i)⁴ = 81
(4i)⁴ = 256
(5i)⁴ = 625
Exponentes de los Números Imaginarios.
Esto es lo que ocurre al Elevar un Número Imaginario (El Patron se repite de la zona azul)
i⁻⁴ = 1
i⁻³ = -i
i⁻² = -1
i⁻¹ = -i
i⁰ = 1
i¹ = i
i² = -1
i³ = -i
i⁴ = 1
i⁵ = i
i⁶ = -1
i⁷ = -i
Mas info del ----> Número Imaginario <----
Con esto Finalizamos la Clasificación de los Números, espero que les haya ayudado un Poco.
Bye :)